
I databehandling är logiska operationer nödvändiga eftersom de kan användas för att modellera hur informationen strömmar genom elektriska kretsar, såsom kretsarna i en CPU. Dessa typer av operationer kallas booleska operationer.
Elementen i en krets som uppför sig enligt Boolean logik kallas logiska grindar.
Grundläggande logiska operationer
Följande sju logiska operationer tar inmatningar som är antingen sanna (1) eller falska (0) och producerar ett enda utmatningsvärde som också är sant eller falskt.
De flesta av dessa operationer kan ta mer än två ingångar, förutom för NOT-funktionen som bara tar en ingång. Nedan följer exempel med endast en eller två ingångar, vilket är vad vanligtvis händer inom en dator.
Verksamheten listas nedan. Klicka på en länk för en operation för att lära dig mer.
- OCH
- ELLER
- INTE
- NAND
- INTE HELLER
- XOR
- XNOR
AND-logikoperationen returnerar endast sant om alla dess ingångar är sanna. Om någon av ingångarna är falsk är utmatningen också falsk.
I datorprogrammering skrivs AND-funktionen vanligtvis som && (två ampersands).
I boolesalgebra kan AND-driften av två ingångar A och B skrivas som AB .
Nedan finns sannoliktabellen för en två-ingångs-EN-drift, och kretsschemat för en OCH-logisk grind.

| OCH | ||
|---|---|---|
en | B | AB |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
ELLER
OR-logikoperationen returnerar sant om någon av dess ingångar är sanna. Om alla ingångar är falska är utmatningen också falsk.
I datorprogrammering skrivs OR-operationen vanligen som || (två vertikala stänger).
I boolesalgebra kan OR-värdet för två ingångar A och B skrivas som A + B.
Obs! Misstas inte OR-funktionen för aritmetisk tillägg, trots att de båda använder symbolen " + ". De är olika verksamheter.
Nedan finns sannoliktabellen för en två-ingångs-OR-operation, och kretsschemat för en OR-logisk grind.

| ELLER | ||
|---|---|---|
en | B | A + B |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
INTE
Den INTE logiska operationen returneras sant om dess ingång är falsk och falsk om dess ingång är sann.
I datorprogrammering skrivs NOT-funktionen vanligen som ! (ett utropstecken).
I Boolean algebra kan INTE-värdet av en ingång A skrivas som A-krona (A med en överskridning).
Nedan finns sannoliktabellen för en NOT-operation, och kretsschemat för en NOT-logisk grind.

NAND
NAND-logikoperationen (som står för "NOT AND") returnerar sant om någon av dess ingångar är falsk och falsk om alla dess ingångar är sanna.
I boolesalgebra kan NAND-värdet av två ingångar A och B skrivas som

NAND har distinktionen att vara en av två "universella" logiska grindar eftersom någon annan logisk operation kan skapas med endast NAND-grindar. (Den andra universella logiska grinden är NOR.)
Nedan finns sannoliktabellen för en två-ingångs NAND-operation, och kretsschemat för en NAND-logikport.

| NAND | ||
|---|---|---|
en | B | ___ AB |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
INTE HELLER
NOR-logikoperationen (som står för "NOT OR") returnerar sant om alla dess ingångar är falska och falska om någon av dess ingångar är sanna.
I boolesalgebra kan NOR-värdet för två ingångar A och B skrivas som
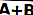
NOR har distinktionen att vara en av två "universella" logiska grindar, eftersom någon annan logisk operation kan skapas med endast NOR-grindar. (Den andra universella logiska grinden är NAND.)
Nedan finns sannolikstabellen för en två-ingångs NOR-drift och kretsschemat för en NOR-logisk grind.

| INTE HELLER | ||
|---|---|---|
en | B | _____ A + B |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
XOR
XOR-logikoperationen (som står för "Exklusiv OR" returnerar sant om någon av dess ingångar skiljer sig åt och falsk om de är alla samma. Med andra ord, om dess ingångar är en kombination av sann och falsk, är XOR-utgångens sant. Om dess ingångar är alla sanna eller alla falska är XOR-utgångens utgång falska.
I boolesalgebra kan XOR-värdet för två ingångar A och B skrivas som A⊕B . (XOR-symbolen, ⊕, liknar ett plustecken i en cirkel.)
Nedan finns sannoliktabellen för en två-ingångs XOR-operation, och dess kretsschema:

| XOR | ||
|---|---|---|
en | B | A⊕B |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
XNOR
XNOR-logikoperationen (som står för "Exklusiv NOT OR" returnerar sant om alla dess ingångar är desamma och falska om någon av dem skiljer sig. Med andra ord, om dess ingångar är en kombination av sann och falsk, XNOR är falskt. Om dess ingångar är alla sanna eller alla falska är XNORs utdata sant.
I boolesalgebra kan XNOR-värdet för två ingångar A och B skrivas som

Nedan finns sannoliktabellen för en två-ingångs XNOR-operation, och dess kretsschema:

| XNOR | ||
|---|---|---|
en | B | _____ A⊕B |
| 0 | 0 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
- Hur skapar jag ett datorprogram?
Ackumulator, Boolean, Idempotence, Operatör, Programmeringsvillkor
